TensorFlow入门
张量(tensor)
Tensorflow中的主要数据单元是张量(tensor), 一个张量包含了一组基本数据,可以是列多维数据。一个张量的"等级"(rank)就是它的维度数字。下面是一些张量例子:
3 # 等级(rank)为0的张量;它是一个标量,形态是[][1., 2., 3.] # 等级为1的张量;它是一个向量,形态是[3][[1., 2., 3.], [4., 5., 6.]] # 等级为2的张量;它是一个矩阵,形态是[2,3][[[1., 2., 3.]], [[7., 8., 9]]] # 等级为3的张量;它的形态是[2, 1, 3]
TensorFlow 核心教程
TensorFlow程序的最重要引用语句如下:
import tensorflow as tf
这样就是使Python能访问TensorFlow的所有类,方法, 标识等。大部分文档都假设你已经引用了。
计算图
你可能认为TensorFlow核心程序作为两个部分的组成:
- 构建计算图
- 运行计算图
计算图是一系列的TensorFlow操作,这些操作被编排到图中各节点上。先来构建一个简单的计算图, 每个节点带有0或者多个输入张量以及一个输出张量。 有一种节点类型是常量。 如所有TensorFlow常量,它没有输入,它的输出一个内部存储的值。我们可以创建两个浮点张量node1和node2如下:
node1 = tf.constant(3.0, dtype=tf.float32)node2 = tf.constant(4.0) # 隐式指定它的类型也是tf.float32print(node1, node2)
最后的打印语句结构是
Tensor("Const:0", shape=(), dtype=float32) Tensor("Const_1:0", shape=(), dtype=float32) 你可能发现,输出并未打印出你所期望的值3.0和4.0。 取而代之是, 它们都是节点, 取值是才会产生3.0和4.0。要实现计算节点值, 我们必须运行Session内的计算图。 一个Session包括TensorFlow的运行时控制与状态。
如下代码创建了一个Session对象, 然后调用了它的run方法取node1和node2的值。运行session中的计算图如下:
sess = tf.Session()print(sess.run([node1, node2]))
我们得到了期望的值3.0和4.0
[3.0, 4.0]
通过组合Tensor节点与操作, 我们可以构建更加复杂的计算。 例如, 我们可以将两常量相加, 产生的新图如下:
node3 = tf.add(node1, node2)print("node3:", node3)print("sess.run(node3):", sess.run(node3)) 最后两打印语句输出:
node3: Tensor("Add:0", shape=(), dtype=float32)sess.run(node3): 7.0 TensorFlow提供了一个功能叫TensorBoard, 它能显示计算图的图形, 下面是一个截图显示TensorBoard是如何可视化计算图的:
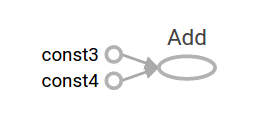
如图所示, 这个图很简单,因为它仅产生一个常量结果, 一个计算图可以参数化来接收外部输入, 它就是占位量(placeholder),一个占位量(placeholder)就是约定了延迟赋值。
a = tf.placeholder(tf.float32)b = tf.placeholder(tf.float32)adder_node = a + b # + 提供了一个tf.add(a,b)的快捷方式
前面的三行有点像一个函数或者一个lambda表达式, 我们定义了两个输入(a和b)以及它们之上的一个操作。我们可以能通过多参输入来计算图值,使用feed_dict参数来填充实际值到占位量(placeholder)。
print(sess.run(adder_node, {a: 3, b: 4.5}))print(sess.run(adder_node, {a:[1, 3], b:[2, 4]})) 输出结果
7.5[3. 7.]
在TensorBoard中, 图形如下:
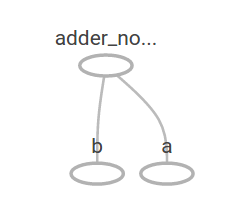
通过添加其它操作,我们可以使计算图更复杂。例如,
add_and_triple = adder_node * 3.print(sess.run(add_and_triple, {a:3, b: 4.5})) 生成输出
22.5
上述的计算图在TensorBoard中显示如下:
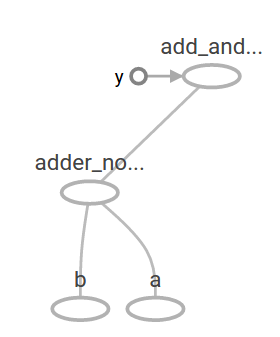
在机器学习中, 我们通常希望模型可以接受任意输入,就是上面的那样。 为了使模型可训练性,我需要能修改计算图,在相同输入情况下,能产生不能的输出。 变量(Variable)使我们可以添加了可训练的参数到图中。我们通过初始值与类型来创建它:
W = tf.Variable ([.3], dtype=tf.float32)b = tf.Variable ([-.3], dtype=tf.float32)x = tf.placeholder(tf.float32)linear_model = W * x + b
常量是在你调用tf.constant时初始化的, 并且这个值永不改变; 相对于变量而言,在你调用tf.Variable的时候并未初始化。 要初始化TensorFlow程序里面的所有变量, 你必须显示的调用如下的特殊操作:
init = tf.global_variables_initializer()sess.run(init)
init是TensorFlow子计算图的句柄,这个非常重要, 它初始化了所有的全局变更。 在我们调用sess.run之前, 这些变量都是未初始化的。
因为x是一个占位量, 我们可以同时计算多个x参数的linear_model值如下:print(sess.run(linear_model, {x: [1, 2, 3, 4]})) 产生了输出是
[0. 0.30000001 0.60000002 0.90000004]
我们创建了一个模型, 但是我们不知道它究竟如何? 我们用训练数据来评估这个模型, 需要一个y占位量(placeholder)来提供一个目标值, 来写一个损失函数。
损失函数用来衡量当前模型与提供的目标值的偏差。对于一个线性模型,我采用一个标准损失模型,它是当前模型值与目标值差的平方和。 linear_model - y 创建了一个向量,它的每一个元素是相应样本的错误偏差, 我们调用tf.square来平方每一个元素。 我们使用tf.reduce_sum来将所有元素求和得到一个标量, 它就是所有样本的总错误。y = tf.placeholder(tf.float32)squared_deltas = tf.square(linear_model - y)loss = tf.reduce_sum(sqared_deltas)print(sess.run(loss, {x: [1, 2, 3, 4], y:[0, -1, -2, -3]})) 产生的损失值为
23.66
通过重新指定W和b的值到刚好-1与1,我们可以手动改善这个损失值。 变量是通过tf.Variable来初始化值,但是我们可以使用像tf.assign这些方法来改变它。 例如, W = -1 and b = 1就是我们这个模型的优化参数。 我们可以分别的改变W和b:
fixW = tf.assign(W, [-1.])fixb = tf.assign(b, [1.])sess.run([fixW, fixb])print(sess.run(loss, {x: [1, 2, 3, 4], y: [0, -1, -2, -3]})) 最终打印显示损失值为0
0.0
我们猜到了W和b的"刚好"值, 但是机器学习的目标就是自动化地找到正确的模型参数。 我们将在下一节展示如何实现它。
tf.train API
完整的机器学习讨论并不在这个教程之内,总之, TensorFlow提供了优化器(optimizer)来慢慢改变每个变量, 以最小化损失函数。最简单的优化器(optimizer)是梯度下降(gradient descent).它根据相应的损失的导数来调整每个变量。总的来说, 手动计算这些导数既乏味又容易出错。因此, TensorFlow能通过函数tf.gradient在仅给定模型描述,自动的产生导数。简单来说, 优化器就是为完成这些,例如:
optimizer = tf.train.GradientDescentOptimizer(0.01)train = optimizer.minimize(loss)
sess.run(init) # 复位缺省值for i in range(1000): sess.run(train, {x: [1,2,3,4], y: [0, -1, -2, -3]})print(sess.run([W, b])) 最终结果参数为:
[array([-0.9999969], dtype=float32), array([ 0.99999082], dtype=float32)]
现在我们就完成了一个实际的机器学习!虽然完成这样一个简单的线性回归不需要太多的TensorFlow核心代码,复杂模型,以及复杂的方法和额外更多的代码来把数据填充到你的模型中。TensorFlow为通用模式,结构,功能提供了一个高层抽象。 我们将在下一节学习如何使用这些中的部分抽象。
完整代码
完整的可训练的线性回归模型展示如下:
import tensorflow as tf# 模型参数W = tf.Variable([.3], dtype=tf.float32)b = tf.Variable([-.3], dtype=tf.float32)# 模型的输入与输出x = tf.placeholder(tf.float32)linear_model = W * x + by = tf.placeholder(tf.float32)# 损失loss = tf.reduce_sum(tf.square(linear_model - y)) # 平方和# 优化器optimizer = tf.GradientDescentOptimizer(0.01)train = optimizer.minize(loss)# 训练数据x_train = [1, 2, 3, 4]y_train = [0, -1, -2, -3]# 训练循环init = tf.global_variables_initializer()sess = tf.Session()sess.run(init) # 初始化为值for i in range(1000): sess.run(train, {x: x_train, y: y_train})# 计算训练准确度curr_W, curr_b, curr_loss = sess.run([w, b, loss], {x: x_train, y: y_train})print("W: %s b: %s loss: %s"%(curr_W, curr_b, curr_loss)) 原文